I believe that the answer Ender put as correct it wrong.
Take this as a summarized example. There are 4 tile types: 1,2,3 & 4. They are laid down in pairs: 1-2 3-4 in row one, and 4-3-2-1 in row two. (see below.)
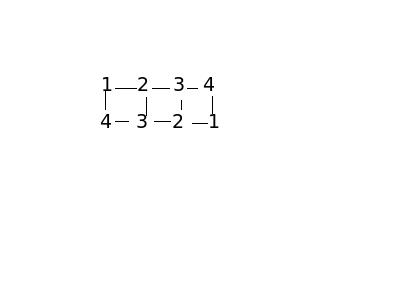
However, 1-2 3-4, 4-3, & 2-1 are not the only pairs there. As shown by the lines in the diagram, there are really 10.
1-2, 2-3, 3-4
4-3, 3-2, 2-1
1 2 3 4
| | | |
4 3 2 1
Therefore, the way used to calculate the answer I believe is false.
Correct.
The solution:

Yes, there are 10 combinations. However the person want three of each pair. When you put 2 pair of tile together in a square:
1 - 2
| |
3 - 4
you get 4 color pairs out of these two pairs of tiles. Taking this into account I do not believe that 60 is the correct answer.
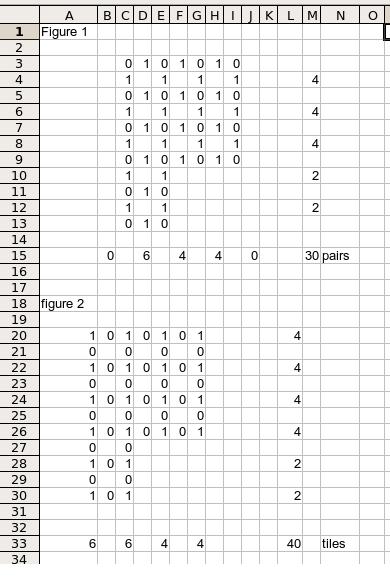
Here is my answer and work (references to figure 1 and 2 refer to the figures at the bottom of the post):
First, I figured out how many possible pairs their were. Like Ender, (5*4)/2, 10 combinations.
Following that I calculated how many pairs, connections between adjacent tiles, would be needed in order to have 3 set of each of the 10 combinations. That is 30 connections.
By changing the dimensions around until i got the 30 connections necessary (see figure 1), I then added the sum of the tiles needed to create that figure 30 connections.
As seen in figure 2, the total number of tiles needed is 40.
EDIT: I counted all the tiles in figure 2 twice, the correct answer therefore is 20.
I believe the correct answer to this problem is
40 20.